Levels in stereo systems, in studio and tape technology

The difficulty of estimating and converting different levels is mainly due to their units. In audio, they are expressed in volts (V), millivolts (mV), microvolts (µV) or decibels (dB). The logarithmic decibel calculation is difficult for many users, although it is used for simplification for calculating, especially between large level differences. This article explains the relationships with calculation examples.

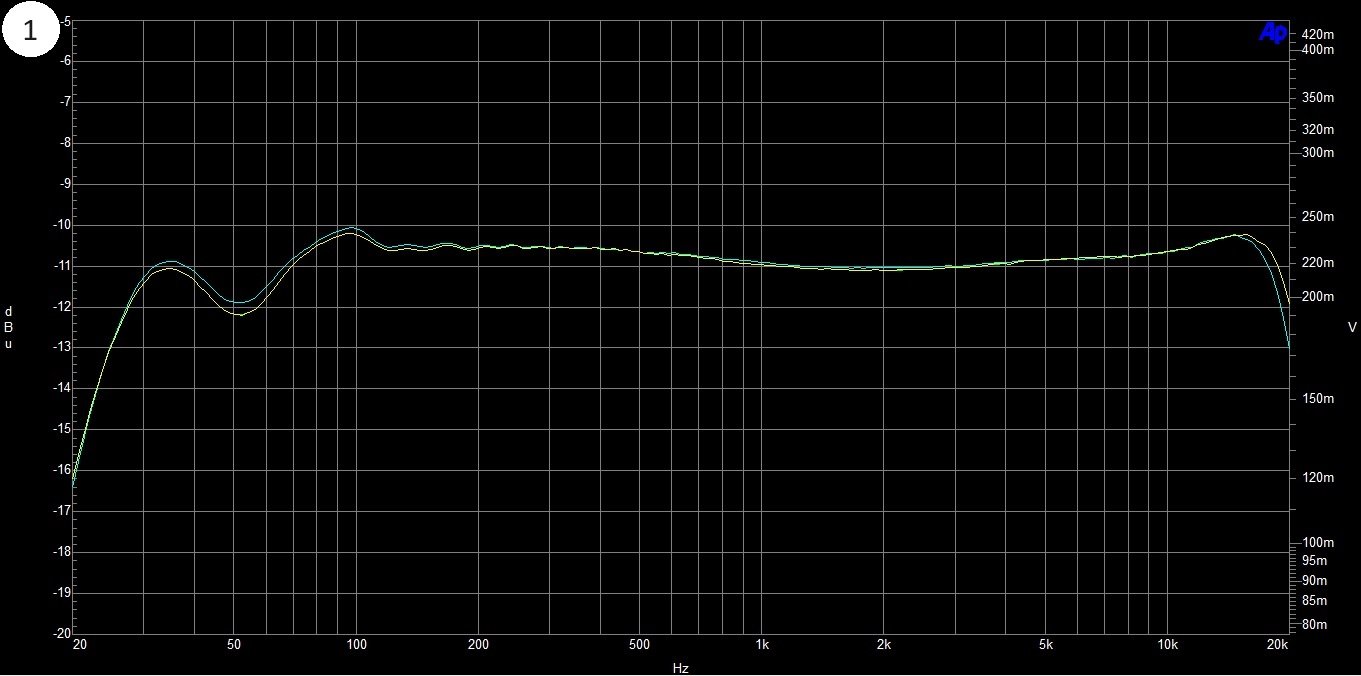
Figure 1: Level curve over band of a Telefunken M15A with 38 cm/s. On the left are the units in dB, on the right the corresponding values in millivolts, below the frequency in Hz; for details see also Figure 2.

See also Table 1: Nanoweber per meter (nWb/m), decibels (dB), voltages (volts), factor and explanation.

0 dBu is a frequently used voltage level, e.g. in recording studio technology. It corresponds to the absolute voltage level of 0.775 volts (line 07 in Table 1). The "u" stands for "unloaded" (without load, or idle), for "unit" (voltage unit), or for "unspecified" (load impedance not specified).

The reference level 0 dBV follows the same rules, the reference value is 1 Volt, for which the "V" stands. Between 0 dBu and 0 dBV there is 2.2 dB. Example: 0 dBu corresponds to -2.2 dBV. If you add 2.2 dB to the value in dBV, you get the value in dBu. Another example: -10 dBV corresponds to -7.8 dBu.

Let's stay with the level in dBu and the voltage in volts. The table illustrates the level ratios in absolute values (dBu and volts) and the factor (the multiplication above 0 dBu or the division below 0 dBu) of the gain with respect to 0 dBu = 0.775 volts:

• +6 dB means a doubling and -6 dB means a halving of the voltage value,

• +20 dB a tenfold and -20 dB a tenfold division of the voltage value.

With the voltage values (Table 1: column D; Fig. 1 right; Fig. 2 right), it is clear that these are difficult to keep track of, partly because of the many decimal places. With the decibel values (Table 1: column C; Fig. 1 left, Fig. 2 left) the calculation becomes easier. Note that above 0 dBu you have to calculate into the positive and below into the negative.

Advantage of the dB-calculation: With the amplification or damping factor one speaks of dB (decibel), which would be impossible with voltage values in this compact form.

The gain or damping factor dB is a relative quantity, the value dBu is an absolute quantity and refers to the fixed value of 0.775 volt.

Example calculations with Table 1 (default values are rounded):

1. A moving coil pickup has an output voltage of 0.31 millivolts (0.00031 volts).

• We find the value in Table 1, line 16, column D.

• The output voltage is -68 dBu.

2. A moving magnet pickup has an output voltage of 3.5 millivolts (0.0035 volts).

• We can find the value in Table 1, line 13, column D.

• The output voltage is -47 dBu

• The level difference of the two pickups is 21 dB

3. A moving magnet phono stage amplifies the signal of the pickup from example 2 with 37 dB

• We calculate: (-47 dBu) + 37 dB = (-10 dBu)

• We find this value in line 09, column C

• The -10 dBu level is a common level for (older) hi-fi equipment.

4. A studio tape recorder has an output level of +6 dBu. By how many dB is the device louder than a source that provides an output voltage of 0.25 volts?

• We find the first value in line 04, the second value in line 09.

• The difference is 16 dB

• We have to "go through zero", comparable to calculating the temperature difference on a thermometer between plus and minus

Level in the tape range

In the tape range, the magnetic flux Φ (Phi) in nWb/m indicates the strength of the magnetic field that can be stored on a tape. This value correlates with the decibel, voltage and factor values of columns C, D and E in Table 1. Double the level means +6 dB as well as a doubling of the magnetic flux. The dB values in between (see rows 05 and 06) can be calculated using the factor. The values of the magnetic flux are often rounded. For example, instead of 514 nWb/m, 510 nWb/m is given. Such small tolerances can be neglected, in this case they correspond to 0.07 dB, smaller than the famous pointer width in analog measuring instruments.

In the tape range, the level world takes place between 0 dBu and +6 dBu, i.e. in a quite small range of 6 dB between 0.77 V and twice the value of 1.55 V. Within this range, you can find practically anything in terms of levels. Many professional master tape copies that can be purchased today are levelled at +6 dBu or 514 mWb/m or even a bit higher, provided that the material is appropriately level-proof. This guarantees a high signal-to-noise ratio. There is nothing wrong with getting a copy with +4 dBu from the USA, if it was pulled 1:1 from the original tape. Such recordings are usually noise-free enough. Devices from the consumer sector get along well with 0 dBu. Even at this level, excellent performance can already be expected. So more does not always help more.